Given a time series of data X, the Autoregressive Integrated Moving Average (ARIMA) model is a tool for understanding and, perhaps, predicting future values in the series. The model consists of three parts, an autoregressive (AR) part, a moving average (MA) part, and an integrated (I) part where an initial differencing step can be applied to remove any non-stationarity in the signal. The model is generally referred to as an ARIMA(p, d, q) model where parameters p, d, and q are non-negative integers that refer to the order of the autoregressive, integrated, and moving average parts of the model respectively.
The ARIMA training function has the following syntax.
arima_train( input_table,
output_table,
timestamp_column,
timeseries_column,
grouping_columns,
include_mean,
non_seasonal_orders,
optimizer_params
)
Arguments
TEXT. The name of the table containing time series data.
TEXT. The name of the table to store the ARIMA model. Three tables are created, with names based on the value of the output_table argument in the training function:
| mean | Model mean (only if 'include_mean' is TRUE) |
|---|---|
| mean_std_error | Standard errors for mean |
| ar_params | Auto-regressions parameters of the ARIMA model |
| ar_std_errors | Standard errors for AR parameters |
| ma_params | Moving average parameters of the ARIMA model |
| ma_std_errors | Standard errors for MA parameters |
| input_table | Table name with the source data |
|---|---|
| timestamp_col | Column name in the source table that contains the timestamp index to data |
| timeseries_col | Column name in the source table that contains the data values |
| non_seasonal_orders | Orders of the non-seasonal ARIMA model |
| include_mean | TRUE if intercept was included in ARIMA model |
| residual_variance | Variance of the residuals |
| log_likelihood | Log likelihood value (when using MLE) |
| iter_num | The number of iterations executed |
| exec_time | Total time taken to train the model |
| timestamp_col | Same as the 'timestamp_col' parameter (all indices from source table included except the first d elements, where d is the differencing order value from 'non_seasonal_orders') |
|---|---|
| residual | Residual value for each data point |
TEXT. The name of the column containing the timestamp (index) data. This could be a serial index (INTEGER) or date/time value (TIMESTAMP).
TEXT. The name of the column containing the time series data. This data is currently restricted to DOUBLE PRECISION.
TEXT, default: NULL. Not currently implemented. Any non-NULL value is ignored.
A comma-separated list of column names used to group the input dataset into discrete groups, training one ARIMA model per group. It is similar to the SQL GROUP BY clause. When this value is null, no grouping is used and a single result model is generated.
BOOLEAN, default: FALSE. Mean value of the data series is added in the ARIMA model if this variable is True.
INTEGER[], default: 'ARRAY[1,1,1]'. Orders of the ARIMA model. The orders are [p, d, q], where parameters p, d, and q are non-negative integers that refer to the order of the autoregressive, integrated, and moving average parts of the model respectively.
The ARIMA forecast function has the following syntax.
arima_forecast( model_table,
output_table,
steps_ahead
)
Arguments
TEXT. The name of the table containing the ARIMA model trained on the time series dataset.
TEXT. The name of the table to store the forecasted values. The output table produced by the forecast function contains the following columns.
| group_by_cols | Grouping column values (if grouping parameter is provided) |
|---|---|
| step_ahead | Time step for the forecast |
| forecast_value | Forecast of the current time step |
SELECT madlib.arima_train();
DROP TABLE IF EXISTS arima_beer; CREATE TABLE arima_beer (time_id integer NOT NULL, value double precision NOT NULL ); COPY arima_beer (time_id, value) FROM stdin WITH DELIMITER '|'; 1 | 93.2 2 | 96.0 3 | 95.2 4 | 77.0 5 | 70.9 6 | 64.7 7 | 70.0 8 | 77.2 9 | 79.5 10 | 100.5 11 | 100.7 12 | 107.0 13 | 95.9 14 | 82.7 15 | 83.2 16 | 80.0 17 | 80.4 18 | 67.5 19 | 75.7 20 | 71.0 21 | 89.2 22 | 101.0 23 | 105.2 24 | 114.0 25 | 96.2 26 | 84.4 27 | 91.2 28 | 81.9 29 | 80.5 30 | 70.4 31 | 74.7 32 | 75.9 33 | 86.2 34 | 98.7 35 | 100.9 36 | 113.7 37 | 89.7 38 | 84.4 39 | 87.2 40 | 85.5 \.
-- Train ARIMA model with 'grouping_columns'=NULL, 'include_mean'=TRUE,
-- and 'non_seasonal_orders'=[1,1,1]
SELECT madlib.arima_train( 'arima_beer',
'arima_beer_output',
'time_id',
'value',
NULL,
FALSE,
ARRAY[1, 1, 1]
);
\x ON SELECT * FROM arima_beer_output;Result:
-[ RECORD 1 ]-+------------------
ar_params | {0.221954769696}
ar_std_errors | {0.575367782602}
ma_params | {-0.140623564576}
ma_std_errors | {0.533445214346}
SELECT * FROM arima_beer_output_summary;Result:
-[ RECORD 1 ]-------+---------------
input_table | arima_beer
timestamp_col | time_id
timeseries_col | value
non_seasonal_orders | {1,1,1}
include_mean | f
residual_variance | 100.989970539
log_likelihood | -145.331516396
iter_num | 28
exec_time (s) | 2.75
\x OFF SELECT * FROM arima_beer_output_residual;Result:
time_id | residual
---------+--------------------
2 | 0
4 | -18.222328834394
6 | -5.49616627282665
...
35 | 1.06298837051437
37 | -25.0886854003757
39 | 3.48401666299571
(40 rows)
SELECT madlib.arima_forecast( 'arima_beer_output',
'arima_beer_forecast_output',
10
);
SELECT * FROM arima_beer_forecast_output;
Result:
steps_ahead | forecast_value
-------------+----------------
1 | 85.3802343659
3 | 85.3477516875
5 | 85.3461514635
7 | 85.3460726302
9 | 85.3460687465
2 | 85.3536518121
4 | 85.3464421267
6 | 85.3460869494
8 | 85.3460694519
10 | 85.34606859
(10 rows)
![\[ (1 - \phi(B)) Y_t = (1 + \theta(B)) Z_t, \]](form_535.png)
where 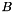 is the backshift operator. The time
is the backshift operator. The time 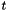 is from
is from 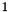 to
to 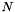 .
.
ARIMA models involve the following variables:
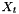 .
.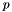 ,
, 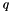 , and
, and 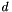 ;
; 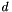 is the differencing order,
is the differencing order, 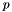 is the order of the AR operator, and
is the order of the AR operator, and 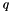 is the order of the MA operator.
is the order of the MA operator.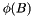 .
.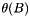 .
.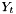 , where
, where 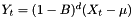 .
.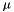 , which is set to be zero for
, which is set to be zero for 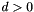 and estimated from the data when d=0.
and estimated from the data when d=0.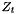 .
.The auto regression operator models the prediction for the next observation as some linear combination of the previous observations. More formally, an AR operator of order 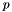 is defined as
is defined as
![\[ \phi(B) Y_t= \phi_1 Y_{t-1} + \dots + \phi_{p} Y_{t-p} \]](form_546.png)
The moving average operator is similar, and it models the prediction for the next observation as a linear combination of the errors in the previous prediction errors. More formally, the MA operator of order 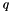 is defined as
is defined as
![\[ \theta(B) Z_t = \theta_{1} Z_{t-1} + \dots + \theta_{q} Z_{t-q}. \]](form_547.png)
We estimate the parameters using the Levenberg-Marquardt Algorithm. In mathematics and computing, the Levenberg-Marquardt algorithm (LMA), also known as the damped least-squares (DLS) method, provides a numerical solution to the problem of minimizing a function, generally nonlinear, over a space of parameters of the function.
Like other numeric minimization algorithms, LMA is an iterative procedure. To start a minimization, the user has to provide an initial guess for the parameter vector, $p$, as well as some tuning parameters 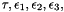 .
.
[1] Rob J Hyndman and George Athanasopoulos: Forecasting: principles and practice, http://otexts.com/fpp/
[2] Robert H. Shumway, David S. Stoffer: Time Series Analysis and Its Applications With R Examples, Third edition Springer Texts in Statistics, 2010
[3] Henri Gavin: The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems, 2011
File arima.sql_in documenting the ARIMA functions