Contents

Clustering refers to the problem of partitioning a set of objects according to some problem-dependent measure of similarity. In the k-means variant, given 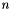$ n $ points 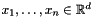$x_1, \dots, x_n \in \mathbb R^d$ , the goal is to position 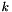$ k $ centroids 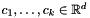$c_1, \dots, c_k \in \mathbb R^d$ so that the sum of distances between each point and its closest centroid is minimized. Each centroid represents a cluster that consists of all points to which this centroid is closest.

Training Function

The k-means algorithm can be invoked in four ways, depending on the source of the initial set of centroids:

Use the random centroid seeding method.

kmeans_random( rel_source,
               expr_point,
               k,
               fn_dist,
               agg_centroid,
               max_num_iterations,
               min_frac_reassigned
             )

Use the kmeans++ centroid seeding method.

kmeanspp( rel_source,
          expr_point,
          k,
          fn_dist,
          agg_centroid,
          max_num_iterations,
          min_frac_reassigned,
          seeding_sample_ratio
        )

Supply an initial centroid set in a relation identified by the rel_initial_centroids argument.

kmeans( rel_source,
        expr_point,
        rel_initial_centroids,
        expr_centroid,
        fn_dist,
        agg_centroid,
        max_num_iterations,
        min_frac_reassigned
      )

Provide an initial centroid set as an array expression in the initial_centroids argument.
```
kmeans( rel_source,
        expr_point,
        initial_centroids,
        fn_dist,
        agg_centroid,
        max_num_iterations,
        min_frac_reassigned
      )
```
Arguments
rel_source

TEXT. The name of the table containing the input data points.

Data points and predefined centroids (if used) are expected to be stored row-wise, in a column of type SVEC (or any type convertible to SVEC, like FLOAT[] or INTEGER[]). Data points with non-finite values (NULL, NaN, infinity) in any component are skipped during analysis.

expr_point

TEXT. The name of the column with point coordinates or an array expression.

k

INTEGER. The number of centroids to calculate.

fn_dist (optional)
TEXT, default: squared_dist_norm2'. The name of the function to use to calculate the distance from a data point to a centroid.

The following distance functions can be used (computation of barycenter/mean in parentheses):
- dist_norm1: 1-norm/Manhattan (element-wise median [Note that MADlib does not provide a median aggregate function for support and performance reasons.])
- dist_norm2: 2-norm/Euclidean (element-wise mean)
- squared_dist_norm2: squared Euclidean distance (element-wise mean)
- dist_angle: angle (element-wise mean of normalized points)
- dist_tanimoto: tanimoto (element-wise mean of normalized points [5])
- user defined function with signature DOUBLE PRECISION[] x, DOUBLE PRECISION[] y -> DOUBLE PRECISION
agg_centroid (optional)
TEXT, default: 'avg'. The name of the aggregate function used to determine centroids.

The following aggregate functions can be used:
- avg: average (Default)
- normalized_avg: normalized average
max_num_iterations (optional)

INTEGER, default: 20. The maximum number of iterations to perform.

min_frac_reassigned (optional)

DOUBLE PRECISION, default: 0.001. The minimum fraction of centroids reassigned to continue iterating. When fewer than this fraction of centroids are reassigned in an iteration, the calculation completes.

seeding_sample_ratio (optional)

DOUBLE PRECISION, default: 1.0. The proportion of subsample of original dataset to use for kmeans++ centroid seeding method. Kmeans++ scans through the data sequentially 'k' times and can be too slow for big datasets. When 'seeding_sample_ratio' is greater than 0 (thresholded to be maximum value of 1.0), the seeding is run on an uniform random subsample of the data. Note: the final K-means algorithm is run on the complete dataset. This parameter only builds a subsample for the seeding and is only available for kmeans++.

rel_initial_centroids

TEXT. The set of initial centroids.

expr_centroid

TEXT. The name of the column (or the array expression) in the rel_initial_centroids relation that contains the centroid coordinates.

initial_centroids

TEXT. A string containing a DOUBLE PRECISION array expression with the initial centroid coordinates.

Output Format

The output of the k-means module is a composite type with the following columns:

centroids	DOUBLE PRECISION[][]. The final centroid positions.
cluster_variance	DOUBLE PRECISION[]. The value of the objective function per cluster.
objective_fn	DOUBLE PRECISION. The value of the objective function.
frac_reassigned	DOUBLE PRECISION. The fraction of points reassigned in the last iteration.
num_iterations	INTEGER. The total number of iterations executed.

Cluster Assignment

After training, the cluster assignment for each data point can be computed with the help of the following function:

closest_column( m, x )

Argument

m: DOUBLE PRECISION[][]. The learned centroids from the training function.
x: DOUBLE PRECISION[]. The data point.

Output format

column_id	INTEGER. The cluster assignment (zero-based).
distance	DOUBLE PRECISION. The distance to the cluster centroid.

Examples

Note: Your results may not be exactly the same as below due to the nature of the k-means algorithm.

Prepare some input data:

DROP TABLE IF EXISTS km_sample;
CREATE TABLE km_sample(pid int, points double precision[]);
INSERT INTO km_sample VALUES
(1,  '{14.23, 1.71, 2.43, 15.6, 127, 2.8, 3.0600, 0.2800, 2.29, 5.64, 1.04, 3.92, 1065}'),
(2,  '{13.2, 1.78, 2.14, 11.2, 1, 2.65, 2.76, 0.26, 1.28, 4.38, 1.05, 3.49, 1050}'),
(3,  '{13.16, 2.36,  2.67, 18.6, 101, 2.8,  3.24, 0.3, 2.81, 5.6799, 1.03, 3.17, 1185}'),
(4,  '{14.37, 1.95, 2.5, 16.8, 113, 3.85, 3.49, 0.24, 2.18, 7.8, 0.86, 3.45, 1480}'),
(5,  '{13.24, 2.59, 2.87, 21, 118, 2.8, 2.69, 0.39, 1.82, 4.32, 1.04, 2.93, 735}'),
(6,  '{14.2, 1.76, 2.45, 15.2, 112, 3.27, 3.39, 0.34, 1.97, 6.75, 1.05, 2.85, 1450}'),
(7,  '{14.39, 1.87, 2.45, 14.6, 96, 2.5, 2.52, 0.3, 1.98, 5.25, 1.02, 3.58, 1290}'),
(8,  '{14.06, 2.15, 2.61, 17.6, 121, 2.6, 2.51, 0.31, 1.25, 5.05, 1.06, 3.58, 1295}'),
(9,  '{14.83, 1.64, 2.17, 14, 97, 2.8, 2.98, 0.29, 1.98, 5.2, 1.08, 2.85, 1045}'),
(10, '{13.86, 1.35, 2.27, 16, 98, 2.98, 3.15, 0.22, 1.8500, 7.2199, 1.01, 3.55, 1045}');

Run k-means clustering using kmeans++ for centroid seeding:

\x on;
SELECT * FROM madlib.kmeanspp( 'km_sample',   -- Table of source data
                               'points',      -- Column containing point co-ordinates 
                               2,             -- Number of centroids to calculate
                               'madlib.squared_dist_norm2',   -- Distance function
                               'madlib.avg',  -- Aggregate function
                               20,            -- Number of iterations
                               0.001          -- Fraction of centroids reassigned to keep iterating 
                             );

Result:

centroids        | {{13.7533333333333,1.905,2.425,16.0666666666667,90.3333333333333,2.805,2.98,0.29,2.005,5.40663333333333,1.04166666666667, 3.31833333333333,1020.83333333333},
                   {14.255,1.9325,2.5025,16.05,110.5,3.055,2.9775,0.2975,1.845,6.2125,0.9975,3.365,1378.75}}
cluster_variance | {122999.110416013,30561.74805}
objective_fn     | 153560.858466013
frac_reassigned  | 0
num_iterations   | 3

Calculate the simplified silhouette coefficient:

SELECT * FROM madlib.simple_silhouette( 'km_sample',
                                        'points',
                                        (SELECT centroids FROM
                                            madlib.kmeanspp('km_sample',
                                                            'points',
                                                            2,
                                                            'madlib.squared_dist_norm2',
                                                            'madlib.avg',
                                                            20,
                                                            0.001)),
                                        'madlib.dist_norm2'
                                      );

Result:

simple_silhouette | 0.686314347664694

Find the cluster assignment for each point:

\x off;
DROP TABLE IF EXISTS km_result;
-- Run kmeans algorithm
CREATE TABLE km_result AS
SELECT * FROM madlib.kmeanspp('km_sample', 'points', 2,
                           'madlib.squared_dist_norm2',
                           'madlib.avg', 20, 0.001); 
-- Get point assignment
SELECT data.*,  (madlib.closest_column(centroids, points)).column_id as cluster_id
FROM km_sample as data, km_result
ORDER BY data.pid;

 pid |                               points                               | cluster_id 
-----+--------------------------------------------------------------------+------------
   1 | {14.23,1.71,2.43,15.6,127,2.8,3.06,0.28,2.29,5.64,1.04,3.92,1065}  |          0
   2 | {13.2,1.78,2.14,11.2,1,2.65,2.76,0.26,1.28,4.38,1.05,3.49,1050}    |          0
   3 | {13.16,2.36,2.67,18.6,101,2.8,3.24,0.3,2.81,5.6799,1.03,3.17,1185} |          0
   4 | {14.37,1.95,2.5,16.8,113,3.85,3.49,0.24,2.18,7.8,0.86,3.45,1480}   |          0
   5 | {13.24,2.59,2.87,21,118,2.8,2.69,0.39,1.82,4.32,1.04,2.93,735}     |          1
   6 | {14.2,1.76,2.45,15.2,112,3.27,3.39,0.34,1.97,6.75,1.05,2.85,1450}  |          0
   7 | {14.39,1.87,2.45,14.6,96,2.5,2.52,0.3,1.98,5.25,1.02,3.58,1290}    |          0
   8 | {14.06,2.15,2.61,17.6,121,2.6,2.51,0.31,1.25,5.05,1.06,3.58,1295}  |          0
   9 | {14.83,1.64,2.17,14,97,2.8,2.98,0.29,1.98,5.2,1.08,2.85,1045}      |          0
  10 | {13.86,1.35,2.27,16,98,2.98,3.15,0.22,1.85,7.2199,1.01,3.55,1045}  |          0
(10 rows)

Run the same example as above, but using array input. Create the input table:

DROP TABLE IF EXISTS km_arrayin CASCADE;
CREATE TABLE km_arrayin(pid int, 
                        p1 float, 
                        p2 float, 
                        p3 float,
                        p4 float, 
                        p5 float, 
                        p6 float,
                        p7 float, 
                        p8 float, 
                        p9 float,
                        p10 float, 
                        p11 float, 
                        p12 float,
                        p13 float);
INSERT INTO km_arrayin VALUES
(1,  14.23, 1.71, 2.43, 15.6, 127, 2.8, 3.0600, 0.2800, 2.29, 5.64, 1.04, 3.92, 1065),
(2,  13.2, 1.78, 2.14, 11.2, 1, 2.65, 2.76, 0.26, 1.28, 4.38, 1.05, 3.49, 1050),
(3,  13.16, 2.36,  2.67, 18.6, 101, 2.8,  3.24, 0.3, 2.81, 5.6799, 1.03, 3.17, 1185),
(4,  14.37, 1.95, 2.5, 16.8, 113, 3.85, 3.49, 0.24, 2.18, 7.8, 0.86, 3.45, 1480),
(5,  13.24, 2.59, 2.87, 21, 118, 2.8, 2.69, 0.39, 1.82, 4.32, 1.04, 2.93, 735),
(6,  14.2, 1.76, 2.45, 15.2, 112, 3.27, 3.39, 0.34, 1.97, 6.75, 1.05, 2.85, 1450),
(7,  14.39, 1.87, 2.45, 14.6, 96, 2.5, 2.52, 0.3, 1.98, 5.25, 1.02, 3.58, 1290),
(8,  14.06, 2.15, 2.61, 17.6, 121, 2.6, 2.51, 0.31, 1.25, 5.05, 1.06, 3.58, 1295),
(9,  14.83, 1.64, 2.17, 14, 97, 2.8, 2.98, 0.29, 1.98, 5.2, 1.08, 2.85, 1045),
(10, 13.86, 1.35, 2.27, 16, 98, 2.98, 3.15, 0.22, 1.8500, 7.2199, 1.01, 3.55, 1045);

Now find the cluster assignment for each point:

DROP TABLE IF EXISTS km_result;
-- Run kmeans algorithm
CREATE TABLE km_result AS
SELECT * FROM madlib.kmeans_random('km_arrayin', 
                                'ARRAY[p1, p2, p3, p4, p5, p6, 
                                      p7, p8, p9, p10, p11, p12, p13]', 
                                2,
                                'madlib.squared_dist_norm2',
                                'madlib.avg', 
                                20, 
                                0.001);
-- Get point assignment
SELECT data.*,  (madlib.closest_column(centroids, 
                                       ARRAY[p1, p2, p3, p4, p5, p6, 
                                      p7, p8, p9, p10, p11, p12, p13])).column_id as cluster_id                                    
FROM km_arrayin as data, km_result
ORDER BY data.pid;

This produces the result in column format:

 pid |  p1   |  p2  |  p3  |  p4  | p5  |  p6  |  p7  |  p8  |  p9  |  p10   | p11  | p12  | p13  | cluster_id 
-----+-------+------+------+------+-----+------+------+------+------+--------+------+------+------+------------
   1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 |  2.8 | 3.06 | 0.28 | 2.29 |   5.64 | 1.04 | 3.92 | 1065 |          0
   2 |  13.2 | 1.78 | 2.14 | 11.2 |   1 | 2.65 | 2.76 | 0.26 | 1.28 |   4.38 | 1.05 | 3.49 | 1050 |          0
   3 | 13.16 | 2.36 | 2.67 | 18.6 | 101 |  2.8 | 3.24 |  0.3 | 2.81 | 5.6799 | 1.03 | 3.17 | 1185 |          0
   4 | 14.37 | 1.95 |  2.5 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 |    7.8 | 0.86 | 3.45 | 1480 |          1
   5 | 13.24 | 2.59 | 2.87 |   21 | 118 |  2.8 | 2.69 | 0.39 | 1.82 |   4.32 | 1.04 | 2.93 |  735 |          0
   6 |  14.2 | 1.76 | 2.45 | 15.2 | 112 | 3.27 | 3.39 | 0.34 | 1.97 |   6.75 | 1.05 | 2.85 | 1450 |          1
   7 | 14.39 | 1.87 | 2.45 | 14.6 |  96 |  2.5 | 2.52 |  0.3 | 1.98 |   5.25 | 1.02 | 3.58 | 1290 |          1
   8 | 14.06 | 2.15 | 2.61 | 17.6 | 121 |  2.6 | 2.51 | 0.31 | 1.25 |   5.05 | 1.06 | 3.58 | 1295 |          1
   9 | 14.83 | 1.64 | 2.17 |   14 |  97 |  2.8 | 2.98 | 0.29 | 1.98 |    5.2 | 1.08 | 2.85 | 1045 |          0
  10 | 13.86 | 1.35 | 2.27 |   16 |  98 | 2.98 | 3.15 | 0.22 | 1.85 | 7.2199 | 1.01 | 3.55 | 1045 |          0
(10 rows)

Notes

The algorithm stops when one of the following conditions is met:

The fraction of updated points is smaller than the convergence threshold (min_frac_reassigned argument). (Default: 0.001).
The algorithm reaches the maximum number of allowed iterations (max_num_iterations argument). (Default: 20).

A popular method to assess the quality of the clustering is the silhouette coefficient, a simplified version of which is provided as part of the k-means module. Note that for large data sets, this computation is expensive.

The silhouette function has the following syntax:

simple_silhouette( rel_source,
                   expr_point,
                   centroids,
                   fn_dist
                 )

Arguments

rel_source: TEXT. The name of the relation containing the input point.
expr_point: TEXT. An expression evaluating to point coordinates for each row in the relation.
centroids: TEXT. An expression evaluating to an array of centroids.
fn_dist (optional): TEXT, default 'dist_norm2', The name of a function to calculate the distance of a point from a centroid. See the fn_dist argument of the k-means training function.

Technical Background

Formally, we wish to minimize the following objective function:

$(c_1, \dots, c_k) \mapsto \sum_{i=1}^n \min_{j=1}^k \operatorname{dist}(x_i, c_j)$

In the most common case, 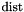$\operatorname{dist}$ is the square of the Euclidean distance.

This problem is computationally difficult (NP-hard), yet the local-search heuristic proposed by Lloyd [4] performs reasonably well in practice. In fact, it is so ubiquitous today that it is often referred to as the standard algorithm or even just the k-means algorithm [1]. It works as follows:

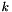Seed the centroids (see below)
Repeat until convergence:
1. Assign each point to its closest centroid
2. Move each centroid to a position that minimizes the sum of distances in this cluster
Convergence is achieved when no points change their assignments during step 2a.

Since the objective function decreases in every step, this algorithm is guaranteed to converge to a local optimum.

Literature

[1] Wikipedia, K-means Clustering, http://en.wikipedia.org/wiki/K-means_clustering

[2] David Arthur, Sergei Vassilvitskii: k-means++: the advantages of careful seeding, Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA'07), pp. 1027-1035, http://www.stanford.edu/~darthur/kMeansPlusPlus.pdf

[3] E. R. Hruschka, L. N. C. Silva, R. J. G. B. Campello: Clustering Gene-Expression Data: A Hybrid Approach that Iterates Between k-Means and Evolutionary Search. In: Studies in Computational Intelligence - Hybrid Evolutionary Algorithms. pp. 313-335. Springer. 2007.

[4] Lloyd, Stuart: Least squares quantization in PCM. Technical Note, Bell Laboratories. Published much later in: IEEE Transactions on Information Theory 28(2), pp. 128-137. 1982.

[5] Leisch, Friedrich: A Toolbox for K-Centroids Cluster Analysis. In: Computational Statistics and Data Analysis, 51(2). pp. 526-544. 2006.

Related Topics

File kmeans.sql_in documenting the k-Means SQL functions

Sparse Vectors

simple_silhouette()